郑州
复习备考
| 业务中心： | 0371-55696552 18037153049 |
您的当前位置：鲁班培训-一建培训,二建培训,监理,注册安全工程师等 > 复习备考 > 模拟试卷 >
利用平衡条件求未知力
作者:admin 来源:未知 浏览: 添加日期：2018-08-03
利用平衡条件求未知力
一、首先介绍几种支座反力悬臂梁中的B点，即固定端支座，其支座反力为：
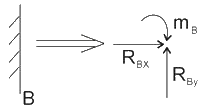B点为固定支座
A点处为固定铰支座，C点处为可动铰支座简支梁中的左侧支座，即固定铰支座，其支座反力为：
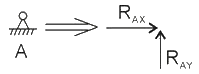
简支梁中的右侧支座，即可动铰支座，其支座反力为：
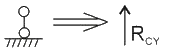
C
二、平衡方程
——ΣX＝0
——ΣY＝0
——ΣM＝0
三、梁的内力：剪力（V）、弯矩（M）
【典型考题】有一简支梁受力与支承如下图，则梁中的弯矩为（ ）kN.m。
A.5
B.6
C.7.5
D.10
[答疑编号5683101201]
『正确答案』A
『答案解析』计算梁内力的一般步骤：第一步，去掉约束，画出杆件受力图。假设A点处有向上的力RAY，水平的力RAX。
第二步：利用平衡方程，求出约束反力。
——ΣX＝0 ＝＞ RAX＝0
——ΣY＝0 ＝＞ RAY+ RBY＝5
——ΣMＡ＝0 ＝＞ 5×2＝RBY×5＝＞ RBY＝2kN，RAY＝3kN
第三步：如需计算梁的内力（剪力或弯矩）可用截面法，取B点至跨中的一段梁作为隔离体，此时应标注出跨中的内力V跨中、M跨中，然后再列平衡方程，可以得出：跨中的弯矩= RBY *5/2=2×2.5=5KN.M
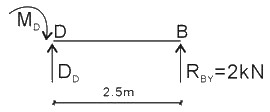
[2005年真题]有一伸臂梁受力及支承如图，则固端A的弯矩为（ ）kN.m。
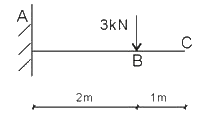
A.2
B.3
C.6
D.9
[答疑编号5683101202]
『正确答案』C
『答案解析』计算梁内力的一般步骤：第一步，去掉约束，画出杆件受力图；
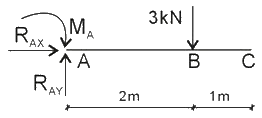
第二步：利用平衡方程，求出约束反力；
——ΣX＝0＝＞RAX＝0
——ΣY＝0＝＞RAY＝3kN
——ΣMA＝0＝＞mA＝3×2＝6kN·m
第三步：用截面法计算出梁的内力。如图所示，固端A的弯矩=3×2=6KN.M
